资料分析 3
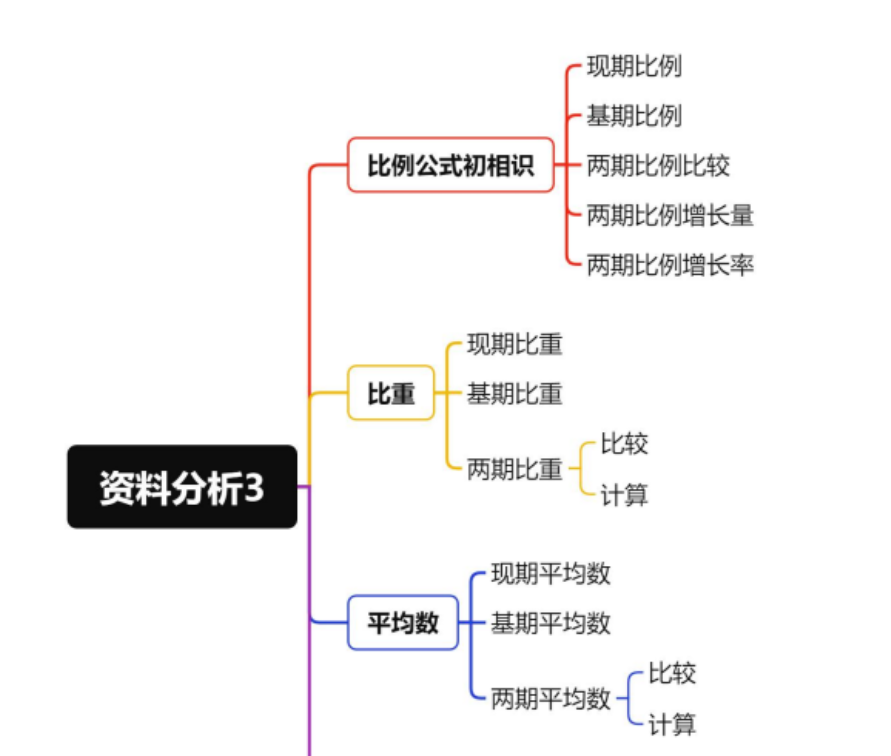
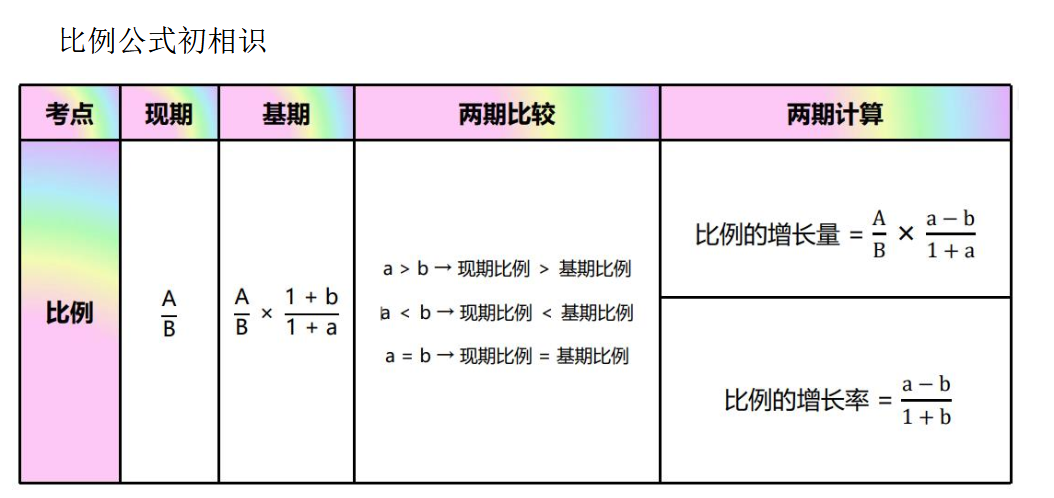
比例
基期比例公式
分子为A,其增长率为a,分母为B,其增长率为b。A/B的基期:
两期比例比较公式
公式
- A 为分子,增长率为 a
- B 为分母,增长率为 b
- 计算当前比例与基期比例的关系。
两期比例变化规律
一般来说占比的一部分的是
- 比较增长率
和 的大小: - 若
,则 现期比例 > 基期比例,表示今年比例同比 上升。 - 若
,则 现期比例 < 基期比例,表示今年比例同比 下降。 - 若
,则 现期比例 = 基期比例,表示今年比例同比 不变。
- 若
总结
- 公式用于 比较现期与基期的比例 变化。
- 只需判断 分子、分母的增长率大小,即可快速得出结论。
配套题目:据对全国 6.4 万家规模以上文化及相关产业企业调查,2021 年前三季度,
上述企业实现营业收入 84205 亿元,按可比口径计算,同比增长 21.8%;两年平均增长 10.0%。分行业类别营业收入情况:
- 新闻信息服务:9847 亿元,同比增长 22.1%
- 内容创作生产:17693 亿元,同比增长 18.6%
- 创意设计服务:13787 亿元,同比增长 24.0%
- 文化传播渠道:9309 亿元,同比增长 30.1%
- 文化投资运营:359 亿元,同比增长 13.8%
- 文化娱乐休闲服务:916 亿元,同比增长 35.3%
- 文化辅助生产和中介服务:11441 亿元,同比增长 18.3%
- 文化装备生产:4880 亿元,同比增长 17.8%
- 文化消费终端生产:15974 亿元,同比增长 22.0%
【例 1】(2023 联考)
与上一年相比,2021 年前三季度分行业类别中,占全国 6.4 万家规模以上文化及相关产业企业营业总收入比重 增加 的行业个数是:
A. 3 个
B. 4 个
C. 5 个
D. 6 个
两期比例的增长量
公式 现期比例 - 基期比例 :
- A 为分子,增长率为 a
- B 为分母,增长率为 b
- 增长量计算为两期比例之差
记忆方法
- 公式与基期比例公式相似,但 分子部分不同。
- 计算增长量时,做差(
),表示比例增长变化量。
📌 总结
- 公式用于 计算现期比例相较基期比例的增长量。
- 只需 计算
的差值,再带入公式计算增长量。
两期比例的增长率
公式
- A 为分子,增长率为 a
- B 为分母,增长率为 b
- 增长率计算为两期比例之比 - 1
记忆方法
- 该公式来源于比例增长率的计算:
- 先计算 现期比例 / 基期比例
- 再 减去 1,得到比例增长率
- 直接做
,然后除以
📌 总结
- 公式用于 计算两期比例的增长率。
- 只需 计算
,然后除以 ,即可得出增长率。
比重
现期比重
- A 为部分数值,B 为总体数值
- 用于计算部分占总体的比例
基期比重
- 计算基期比重时,部分与总体的增长率需要分别调整。
两期比重差(增长量)
- 用于计算两期比重的差异
- 只需计算
,再除以
方法:口算 **,
判断升降:
结果为正,今年比重同比上升;
结果为负,今年比重同比下降。
算多少:
结果的绝对值 <| a- b | , 满足选项只有一个,当选。
满足选项多个,补全公式分析计算。
举例解释
例子 1:某行业的比重变化
假设:
- 2023 年,某行业 A 的收入占全国总收入的比重为 30%(即 AB=0.3\frac{A}{B} = 0.3)。
- 2024 年,行业 A 的收入增长了 20%,全国总收入增长了 25%。
那么:
- 行业 A 的增长率 a=20%=0.2a = 20% = 0.2
- 全国收入的增长率 b=25%=0.25b = 25% = 0.25
- 原始比重 AB=0.3\frac{A}{B} = 0.3
根据两期比重计算公式:
比重差=AB×a−b1+a\text{比重差} = \frac{A}{B} \times \frac{a - b}
代入数据计算:
比重差=0.3×0.2−0.251+0.2\text{比重差} = 0.3 \times \frac{0.2 - 0.25}{1 + 0.2} =0.3×−0.051.2= 0.3 \times \frac{-0.05}{1.2} =0.3×(−0.0417)= 0.3 \times (-0.0417) =−0.0125= -0.0125
结果是负数,说明行业 A 在 2024 年的比重下降,下降 1.25%。
例题 1:
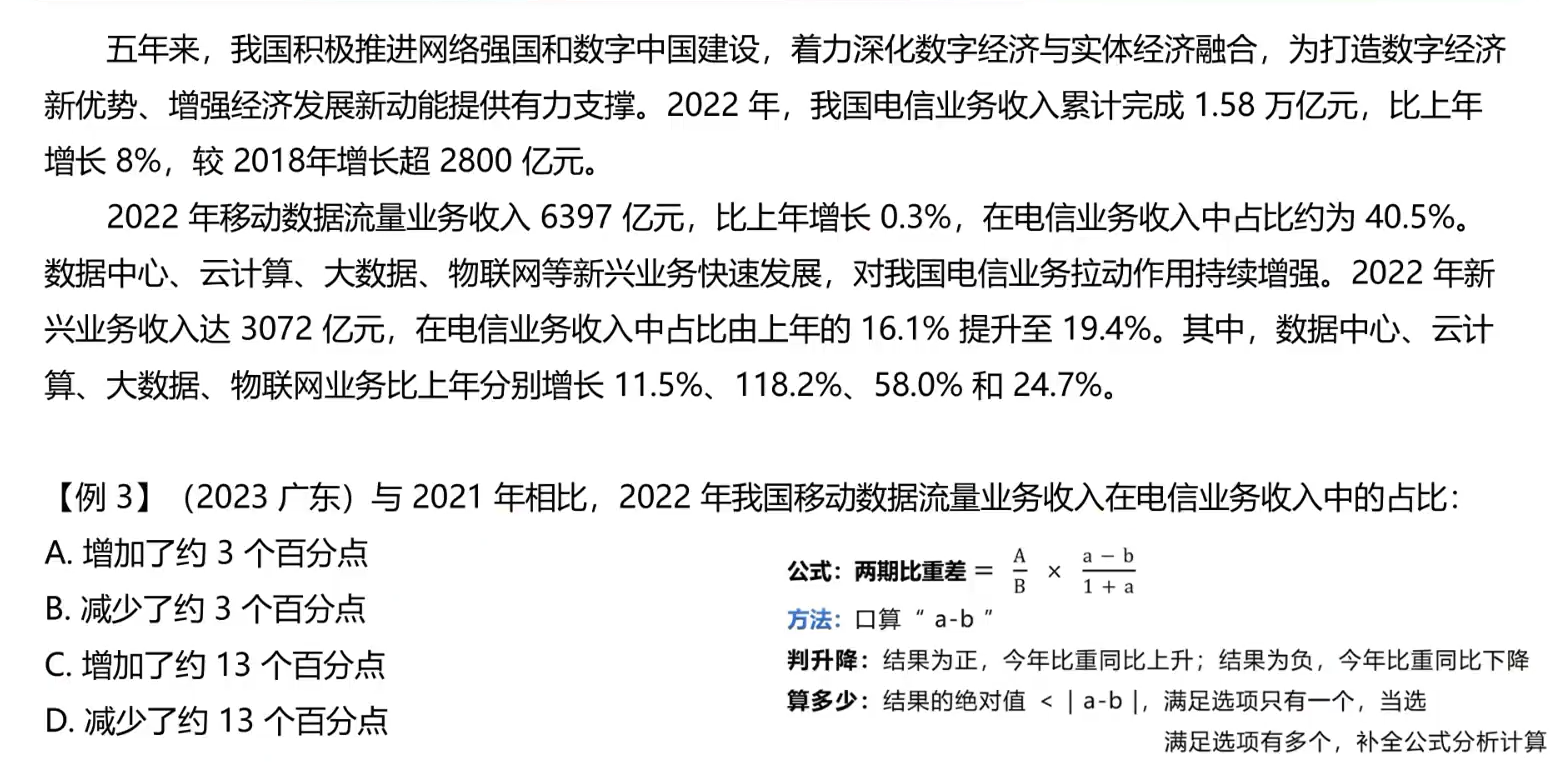
这一类题是可以直接看 a 和 b 的关系,通过a - b的结果来看增加或者减少,结合选项得出结论。
例题 2

找到 a 和 b , 然后找到A/B,结合公式得出两期比重差。
例题3:
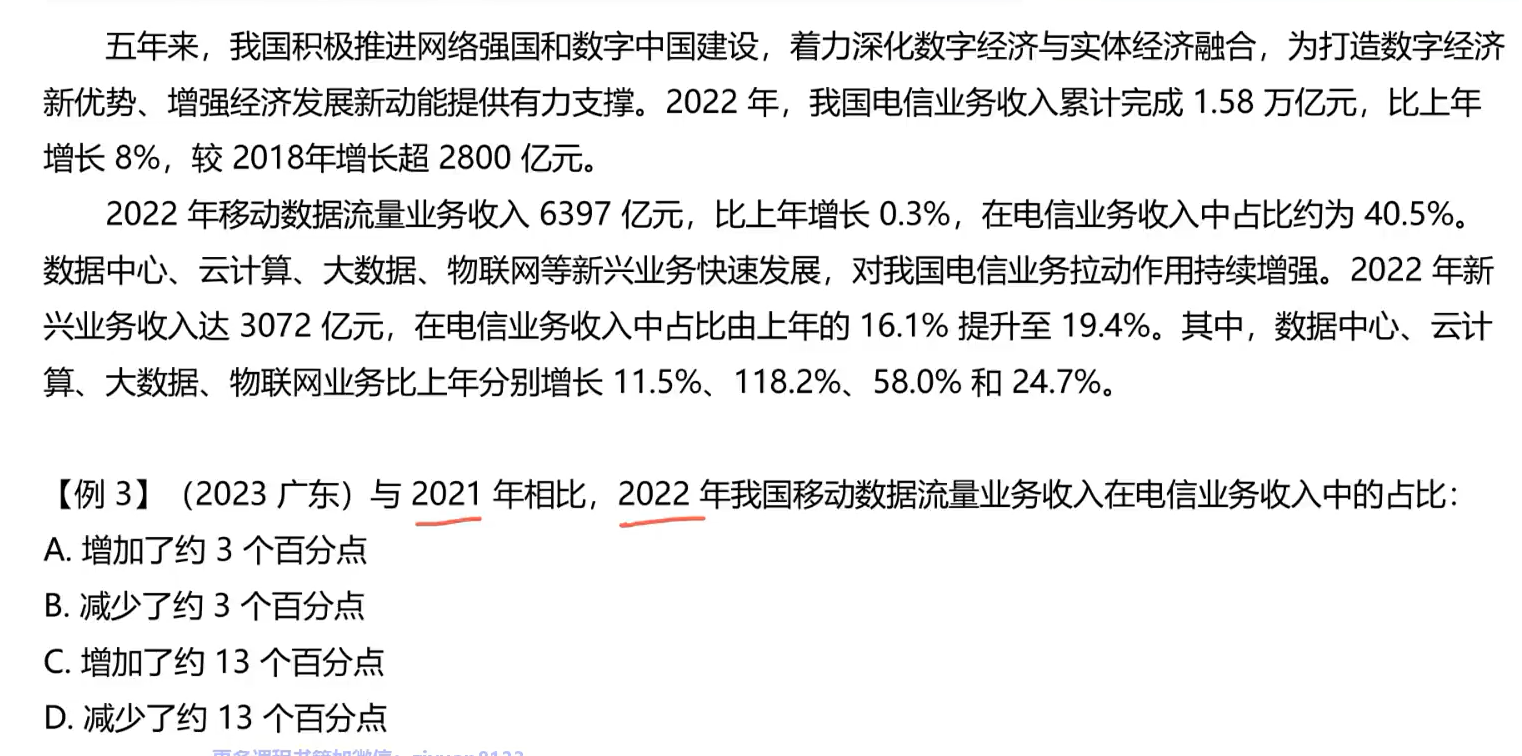
相关概念
- 利润率:
- 增长贡献率:
总结
- 公式主要用于 比重计算,可应用于 利润率、市场占比、贡献率等场景。
- 增长率的调整 是基期比重计算的关键。
现期比重:求总体
公式
认知过程
- 识别 时间
- 识别 现期
- 识别 关键字
- 识别 比重
- 使用公式计算 总体
示例
| 部分 | 比重 | 总体计算 | 结果 |
|---|---|---|---|
| 2024年志哥收入为 20 元 | 占家庭总收入 20% | 总体 = 20 ÷ 20% | 100 元 |
现期比重:求部分
公式
认知过程
- 识别 时间
- 识别 现期
- 识别 总体
- 识别 比重
- 使用公式计算 部分
**示例
| 总体 | 比重 | 部分计算 | 结果 |
|---|---|---|---|
| 2024年志哥家庭总收入 100 元 | 志哥收入占 20% | 部分 = 100 × 20% | 20 元 |
现期比重:饼图

计算技巧

平均数
关键词: 均、每、单位面积、单位企业
平均数的公式总结
1. 现期平均数
情况一 正常表述 后 ➗ 前
情况二 倒装表述,单位的量做分子
情况三 出现月均,日均的双重平均,优先除以时间,再平均
情况四 求多个数的平均值 数据相差大,加上之后直接除;
数据相差小,削峰填谷。
例题一

前20的企业,平均每家每月收入:
那么就是 上半年的收入除以6,然后除以20
2. 基期平均数
选项差距大,2位约分。
选项差距小,3位化1。
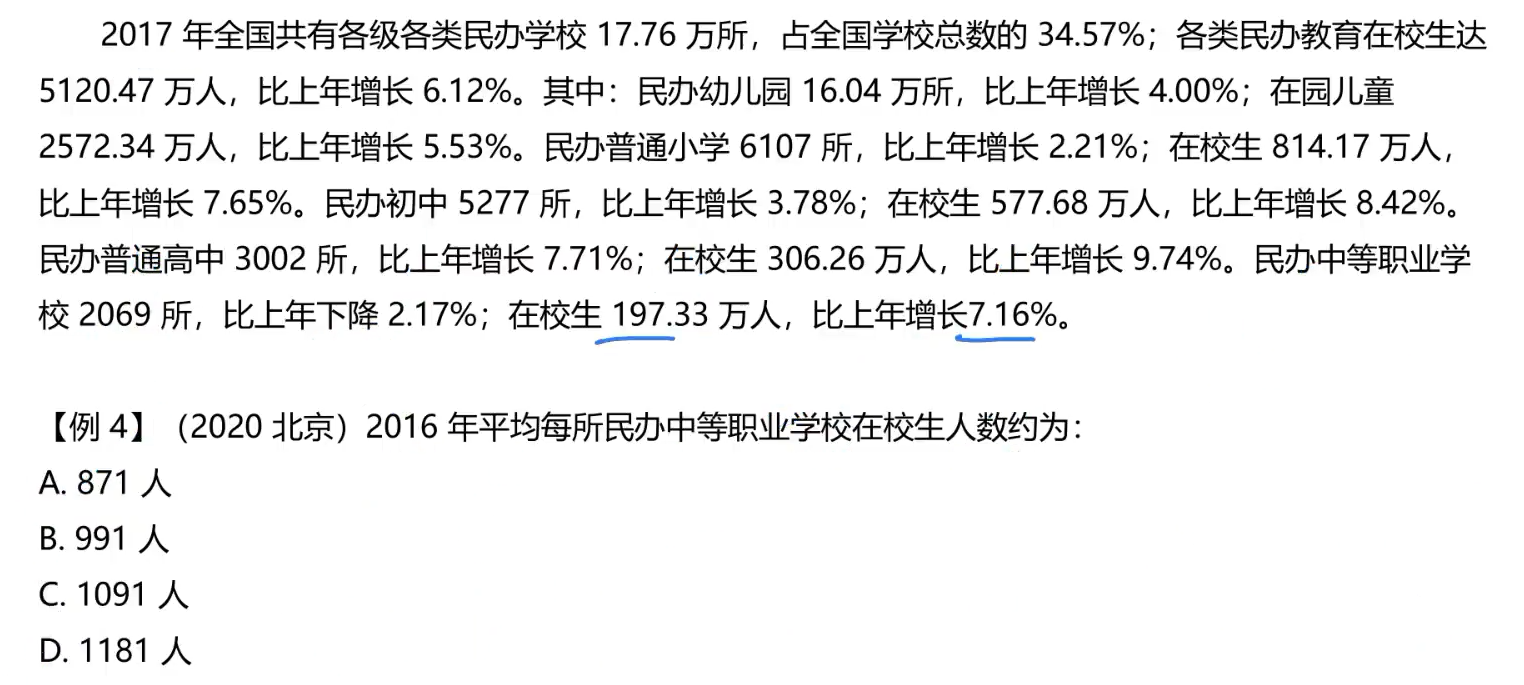
B为总数,b为总量增减率。A为部分,a为部分增减率。
带入公式计算。
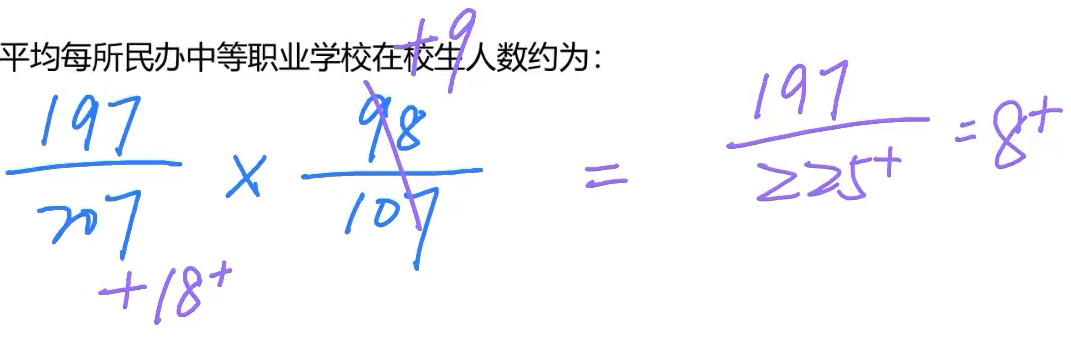
左边的分数和右边的分数可以这样来操作,右边的98加9,可以刚好和分母107变成1,98和207的倍数约等于2,于是207可以加18来消除差异(大约)。
然后197除以225,等于8开头的,选择A
**3. 两期平均数的增长量 **
和 两期比重差(增长量)一样
认知过程
时间 → 两个 → 两期 → 关键词 “均” → 两期平均数 → 上升/下降 + 单位 → 平均数的增长量
房子销售= 钱除以面积
例题:

4. 两期平均数的增长率
方法
- 快速估算:口算 a−b
- 判断上升/下降:
- 结果为正:今年平均数 同比上升
- 结果为负:今年平均数 同比下降
判断增长幅度
- 看 b 的符号
- b>0(基期增长):结果的绝对值 小于 ∣a−b∣
- b<0(基期下降):结果的绝对值 大于 ∣a−b∣
经验:后a,前b。
两期平均数比较总结
1. 认知过程
时间 → 两个 → 两期 → 关键词 均 → 上升/下降 → 两期平均数比较
2. 方法
- 比较分子增长率 a 与分母增长率 b
- 经验法则:后 a,前 b
3. 结论
- a>b → 现期平均数 > 基期平均数 → 同比上升
- a<b → 现期平均数 < 基期平均数 → 同比下降
- a=b → 现期平均数 = 基期平均数 → 同比不变
4. 例子
2017 年,S 市服务业小微样本企业每万元营业收入缴纳营业税金及附加同比变化情况:
- 若 企业收入增长率 a 高于税费增长率 b → 税费占收入比下降
- 若 企业收入增长率 a 低于税费增长率 b → 税费占收入比上升
例题:

提示:平均数的增长率只跟小a和小b有关系,大A和大B都没关系。
然后记住a在后,b在前。
或者用口算的方法
a-b
例题2

平均数导图
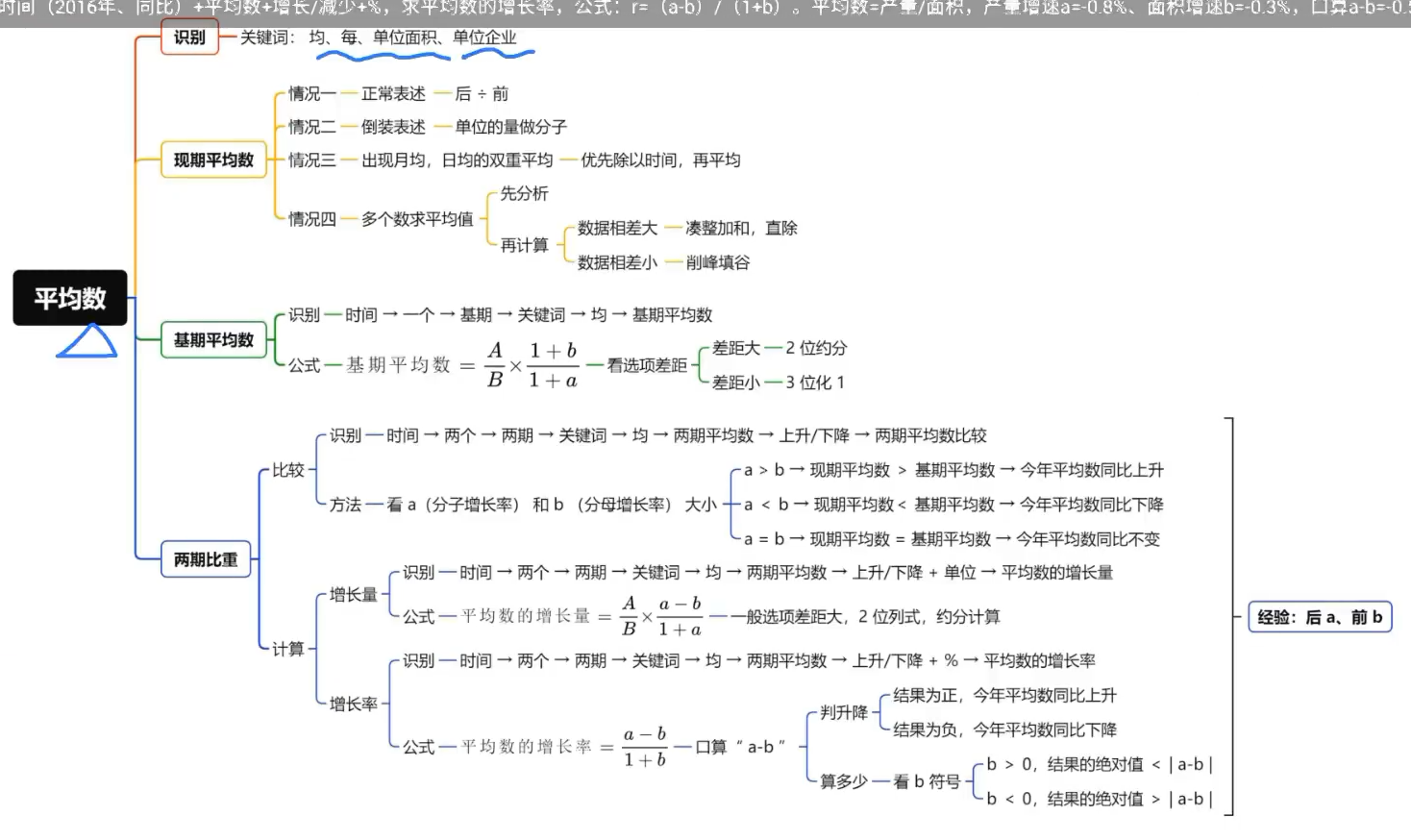
平均数的倍数
认知过程:
时间 → 一个 → 现期 → 关键词 → 倍 → 现期倍数 → 主体 → 平均数 → 平均数的倍数
公式:
方法:
- 弄清分子、分母(后 ÷ 前)
- 口算分子倍数,口算分母倍数
- 计算平均数的倍数:
例题:
